数学建模更新16(粒子群算法)
本文共 26871 字,大约阅读时间需要 89 分钟。
粒子群算法
一.概述
1.概念
通过模拟鸟群觅食行为而发展起来的一种基于群体协作的搜索算法。其用于求解函数的最值问题。
2.启发式算法
启发式算法百度百科上的定义:一个基于直观或经验构造的算法,在可接受的花费下给出待解决优化问题的一个可行解。
1. 什么是可接受的话费? 计算时间和空间能接受(求解一个问题要几万年 or 一万台电脑) 2. 什么是优化问题? 工程设计中优化问题(optimization problem)指在一定约束条件下,求解一个目标函数的最大值(或最小值)问题。 注:实际上和我们之前学过的规划问题的定义一样,称呼不同而已 3.什么是可行解? 得到的结果能用于工程实践(不一定非要是最优解)常见的启发式算法:
粒子群、模拟退火、遗传算法、蚁群算法、禁忌搜索算法等等 (启发式算法解决的问题大同小异,只要前三个算法学会了在数学建模中就足够了)
二.最简单的优化问题
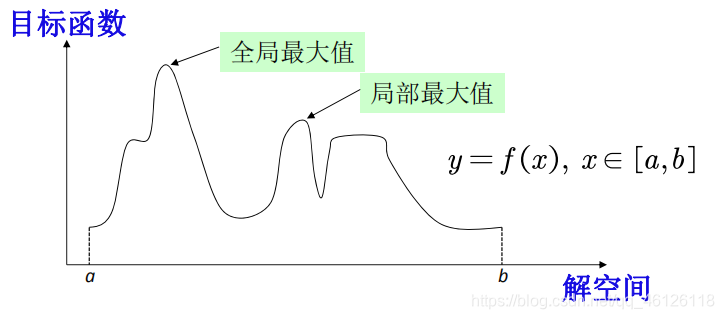
1.盲目搜索法

2.启发式搜索

三.粒子群算法
1.思想
它的核心思想是利用群体中的个体对信息的共享使
整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。2.直观解释
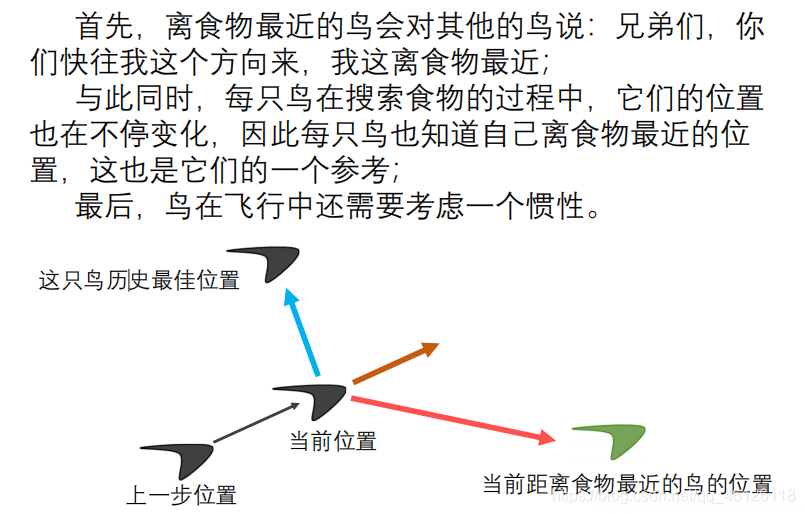
3.基本概念
- 粒子:优化问题的候选解
- 位置:候选解所在的位置
- 速度:候选解移动的速度
- 适应度:评价粒子优劣的值,一般设置为目标函数值
- 个体最佳位置:单个例子迄今为止找到的最佳位置
- 群体最佳位置:所有例子迄今为止找到的最佳位置
4.粒子群算法流程图
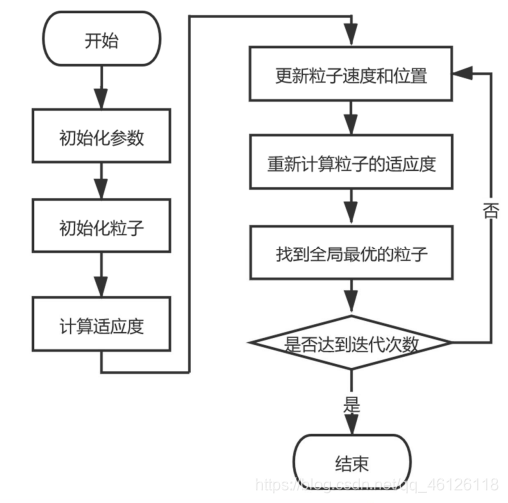
5.符号说明
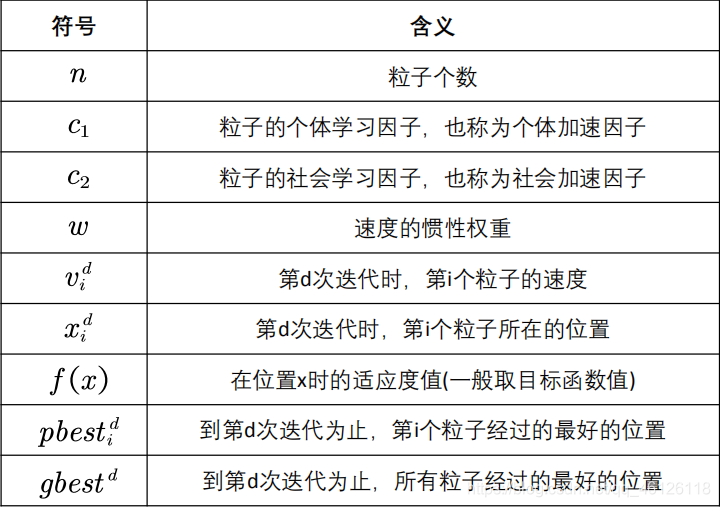
6.核心公式
这只鸟第d步的速度 =上一步自身的速度惯性 + 自我认知部分 +社会认知部分
$v(d) = w* v(d‐1) + c1* r1* (pbest(d)‐x(d)) + c2* r2* (gbest(d)‐x(d)) $ (三个部分的和)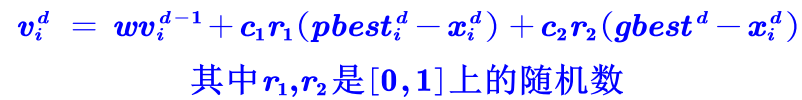
这只鸟第d+1步所在的位置 = 第d步所在的位置 + 第d步的速度 * 运动的时间
x ( d + 1 ) = x ( d ) + v ( d ) ∗ t x(d+1) = x(d) + v(d) * t x(d+1)=x(d)+v(d)∗t (每一步运动的时间t一般取1)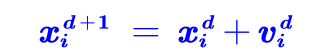
四.粒子群算法的参数
1.学习因子

2.惯性权重
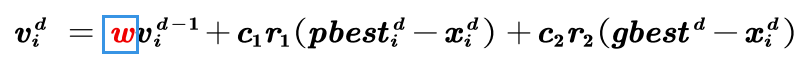
五.求一元函数的最大值
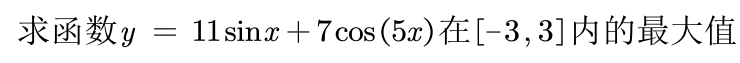
%% 绘制函数的图形x = -3:0.01:3;y = 11*sin(x) + 7*cos(5*x);figure(1)plot(x,y,'b-')title('y = 11*sin(x) + 7*cos(5*x)')hold on % 不关闭图形,继续在上面画图 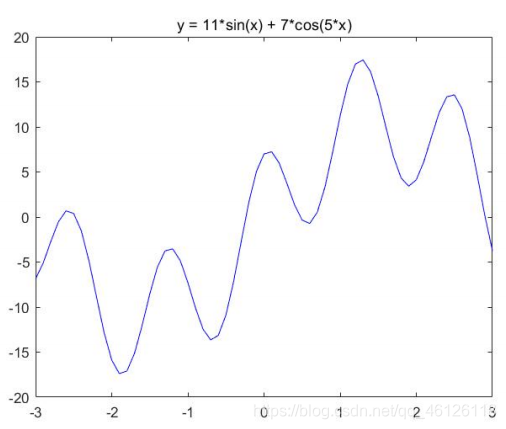
1.之前学过的线性回归方式
%% 求解函数y = 11*sin(x) + 7*cos(5*x)在[-3,3]内的最大值x0 = 0; A=[]; b=[];Aeq=[];beq=[];x_lb = -3; % x的下界x_ub = 3; % x的上界[x,fval] = fmincon(@Obj_fun1,x0,A,b,Aeq,beq,x_lb,x_ub)fval = -fval% x = 1.2750, y = 17.4928% 如果把初始值改为x0 = 2,结果会是什么?

2.粒子群算法参数
【1】设置参数
n = 10; % 粒子数量narvs = 1; % 变量个数(函数中有几个自变量)c1 = 2; % 每个粒子的个体学习因子c2 = 2; % 每个粒子的社会学习因子w = 0.9; % 惯性权重K = 50; % 迭代的次数vmax = 1.2; % 粒子的最大速度x_lb = -3; % x的下界x_ub = 3; % x的上界
(1) 增加粒子数量会增加我们找到更好结果的可能性,但会增加运算的时间。
(2) c1,c2,w这三个量有很多改进空间 (3) 迭代的次数K越大越好吗?不一定哦,如果现在已经找到最优解了,再增加迭代次数是没有意义的。 (4) 这里出现了粒子的最大速度,是为了保证下一步的位置离当前位置别太远,一般取自变量可行域的10%至20%(不同文献看法不同)。 (5) X的下界和上界是保证粒子不会飞出定义域
【2】初始化粒子的位置和速度
x = zeros(n,narvs);for i = 1: narvs% 随机初始化粒子所在的位置在定义域内x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); end% 随机初始化粒子的速度,设置为[-vmax,vmax]v = -vmax + 2*vmax .* rand(n,narvs);

【3】计算适应度
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度fit(i) = Obj_fun1(x(i,:)); % 调用Obj_fun1函数来计算适应度(这里写成x(i,:)主要是为了和以后遇到的多元函数互通)endpbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == max(fit), 1); % 找到适应度最大的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)function y = Obj_fun1(x)y = 11*sin(x) + 7*cos(5*x);end
注意:
(1)这里的适应度实际上就是我们的目标函数值。 (2)这里可以直接计算出pbest和gbest,在后面将用于计算粒子的速度以更新粒子的位置。
【4】循环体:更新粒子速度和位置
for d = 1:K % 开始迭代,一共迭代K次for i = 1:n % 依次更新第i个粒子的速度与位置% 更新第i个粒子的速度v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 如果粒子的速度超过了最大速度限制,就对其进行调整for j = 1: narvsif v(i,j) < -vmax(j)v(i,j) = -vmax(j);elseif v(i,j) > vmax(j)v(i,j) = vmax(j);endendx(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置% 如果粒子的位置超出了定义域,就对其进行调整for j = 1: narvsif x(i,j) < x_lb(j)x(i,j) = x_lb(j);elseif x(i,j) > x_ub(j)x(i,j) = x_ub(j);endend
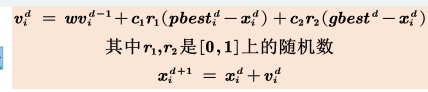
【5】重新计算适应度并找到最优粒子
fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度% 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度if fit(i) > Obj_fun1(pbest(i,:)) pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置end% 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度if Obj_fun1(pbest(i,:)) > Obj_fun1(gbest)gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置endendend
【6】粒子群算法运行的结果
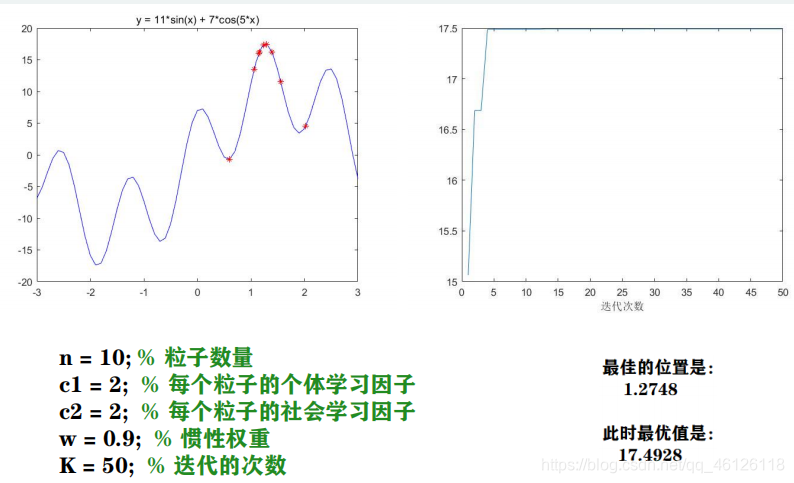
【7】代码汇总
%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度 % 如果粒子的速度超过了最大速度限制,就对其进行调整 for j = 1: narvs if v(i,j) < -vmax(j) v(i,j) = -vmax(j); elseif v(i,j) > vmax(j) v(i,j) = vmax(j); end end x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun1(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) > Obj_fun1(pbest(i,:)) % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) > Obj_fun1(gbest) % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun1(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x; % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = fit; % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化)endfigure(2)plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun1(gbest)) 六.例2:求二元函数的最小值
1.原始方法
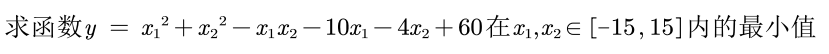
注意: 用粒子群算法求解函数最小值时,粒子适应度的计算我们仍设置为目标函数值,但是此时我们希望找到适应度最小的解。因此希望大家不要用
我们中文的内涵去理解这里的“适应度” (中文的内涵就是越适应越好),为了避免混淆你可以就直接用目标函数值来代替适应度的说法。
%% 粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图 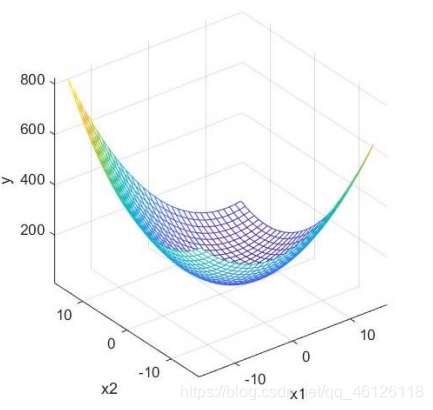
%% 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值x0 = [0 0]; A=[]; b=[];Aeq=[];beq=[];x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界[x,fval] = fmincon(@Obj_fun2,x0,A,b,Aeq,beq,x_lb,x_ub)

2.改进:线性递减惯性权重
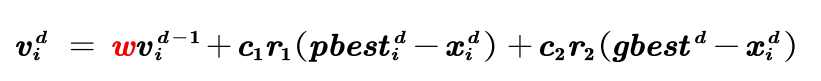
 与原来的相比,现在惯性权重和迭代次数有关
与原来的相比,现在惯性权重和迭代次数有关 3.三种递减惯性权重的图形
w_start = 0.9; w_end = 0.4; K = 30; d = 1:K; w1 = w_start-(w_start-w_end)*d/K;w2 = w_start-(w_start-w_end)*(d/K).^2;w3 = w_start-(w_start-w_end)*(2*d/K-(d/K).^2);plot(d,w1,'r',d,w2,'b',d,w3,'g'); legend('w1','w2','w3') 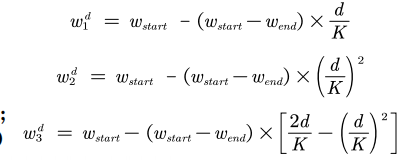

%% 线性递减惯性权重的粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)n = 30; % 粒子数量narvs = 2; % 变量个数c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数w_start = 0.9; % 初始惯性权重,通常取0.9w_end = 0.4; % 粒子群最大迭代次数时的惯性权重,通常取0.4K = 100; % 迭代的次数vmax = [6 6]; % 粒子的最大速度x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 在图上标上这n个粒子的位置用于演示h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 w = w_start - (w_start - w_end) * d / K; v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度 % 如果粒子的速度超过了最大速度限制,就对其进行调整 for j = 1: narvs if v(i,j) < -vmax(j) v(i,j) = -vmax(j); elseif v(i,j) > vmax(j) v(i,j) = vmax(j); end end x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化) h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun2(gbest))%% 三种递减惯性权重的对比w_start = 0.9; w_end = 0.4; K = 30; d = 1:K; w1 = w_start-(w_start-w_end)*d/K;w2 = w_start-(w_start-w_end)*(d/K).^2;w3 = w_start-(w_start-w_end)*(2*d/K-(d/K).^2);figure(3)plot(d,w1,'r',d,w2,'b',d,w3,'g'); legend('w1','w2','w3') 4.改进:自适应惯性权重
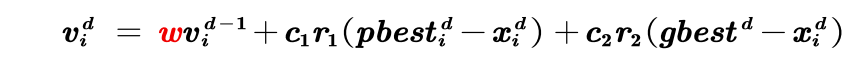

一个较大的惯性权值有利于全局搜索 而一个较小的权值则更利于局部搜索



一个较大的惯性权值有利于全局搜索 而一个较小的权值则更利于局部搜索
假设现在一共五个粒子ABCDE,此时它们的适应度分别为1, 2, 3, 4, 5
取最大惯性权重为0.9,最小惯性权重为0.4 那么,这五个粒子的惯性权重应该为:0.9, 0.9, 0.9,0.65, 0.4 适应度越小,说明距离最优解越远,此时更需要全局搜索 适应度越大,说明距离最优解越近,此时更需要局部搜索%% 自适应权重的粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)n = 30; % 粒子数量narvs = 2; % 变量个数c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数w_max = 0.9; % 最大惯性权重,通常取0.9w_min = 0.4; % 最小惯性权重,通常取0.4K = 100; % 迭代的次数vmax = [6 6]; % 粒子的最大速度x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 在图上标上这n个粒子的位置用于演示h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 f_i = fit(i); % 取出第i个粒子的适应度 f_avg = sum(fit)/n; % 计算此时适应度的平均值 f_min = min(fit); % 计算此时适应度的最小值 if f_i <= f_avg if f_avg ~= f_min % 如果分母为0,我们就干脆令w=w_min w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min); else w = w_min; end else w = w_max; end v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度 % 如果粒子的速度超过了最大速度限制,就对其进行调整 for j = 1: narvs if v(i,j) < -vmax(j) v(i,j) = -vmax(j); elseif v(i,j) > vmax(j) v(i,j) = vmax(j); end end x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化) h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun2(gbest)) 5.改进:随机惯性权重
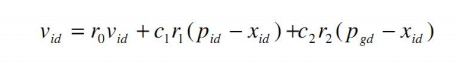

%% 随机权重的粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)n = 30; % 粒子数量narvs = 2; % 变量个数c1 = 2; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2; % 每个粒子的社会学习因子,也称为社会加速常数w_max = 0.9; % 最大惯性权重,通常取0.9w_min = 0.4; % 最小惯性权重,通常取0.4sigma = 0.3; % 正态分布的随机扰动项的标准差(一般取0.2-0.5之间)K = 100; % 迭代的次数vmax = [6 6]; % 粒子的最大速度x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 在图上标上这n个粒子的位置用于演示h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 w = w_min + (w_max - w_min)*rand(1) + sigma*randn(1); v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度 % 如果粒子的速度超过了最大速度限制,就对其进行调整 for j = 1: narvs if v(i,j) < -vmax(j) v(i,j) = -vmax(j); elseif v(i,j) > vmax(j) v(i,j) = vmax(j); end end x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化) h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun2(gbest)) 6.改进:压缩(收缩)因子法
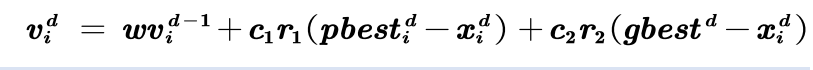
7.改进:压缩因子法
压缩因子法中应用较多的个体学习因子c1和社会学习因子c2均取2.05,
用我们自己的符号可以表示为:
%% 带有压缩因子(收缩因子)的粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)n = 30; % 粒子数量narvs = 2; % 变量个数c1 = 2.05; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2.05; % 每个粒子的社会学习因子,也称为社会加速常数C = c1+c2; fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子w = 0.9; % 惯性权重 K = 100; % 迭代的次数vmax = [6 6]; % 粒子的最大速度x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 在图上标上这n个粒子的位置用于演示h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:))); % 更新第i个粒子的速度 % 有时候会看到直接写成:0.657*v(i,:) + 1.496*rand(1)*(pbest(i,:) - x(i,:)) + 1.496*rand(1)*(gbest - x(i,:))); x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化) h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun2(gbest)) 8.改进:非对称学习因子

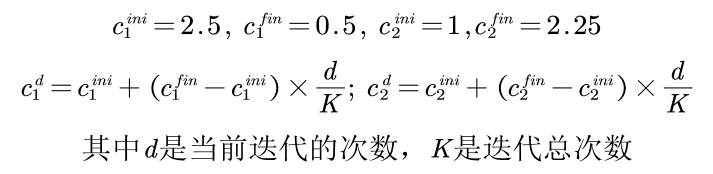
c1_ini = 2.5; % 个体学习因子的初始值c1_fin = 0.5; % 个体学习因子的最终值c2_ini = 1; % 社会学习因子的初始值c2_fin = 2.25; % 社会学习因子的最终值……for d = 1:K % 开始迭代,一共迭代K次c1 = c1_ini + (c1_fin - c1_ini)*d/K;c2 = c2_ini + (c2_fin - c2_ini)*d/K;for i = 1:n % 依次更新第i个粒子的速度与位置% 更新第i个粒子的速度v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); ……
%% 非对称学习因子的粒子群算法PSO: 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(动画演示)clear; clc% 毛开富, 包广清, 徐驰. 基于非对称学习因子调节的粒子群优化算法[J]. 计算机工程, 2010(19):188-190.(公式10中的减号应该改为加号)%% 绘制函数的图形x1 = -15:1:15;x2 = -15:1:15;[x1,x2] = meshgrid(x1,x2);y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;mesh(x1,x2,y)xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示hold on % 不关闭图形,继续在上面画图%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)n = 30; % 粒子数量narvs = 2; % 变量个数c1_ini = 2.5; % 个体学习因子的初始值c1_fin = 0.5; % 个体学习因子的最终值c2_ini = 1; % 社会学习因子的初始值c2_fin = 2.25; % 社会学习因子的最终值w = 0.9; % 惯性权重K = 100; % 迭代的次数vmax = [6 6]; % 粒子的最大速度x_lb = [-15 -15]; % x的下界x_ub = [15 15]; % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun2(x(i,:)); % 调用Obj_fun2函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 在图上标上这n个粒子的位置用于演示h = scatter3(x(:,1),x(:,2),fit,'*r'); % scatter3是绘制三维散点图的函数(这里返回h是为了得到图形的句柄,未来我们对其位置进行更新)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 % w = 0.9 - 0.5*d/K; % 效果不是很好的话可以同时考虑线性递减权重 c1 = c1_ini + (c1_fin - c1_ini)*d/K; c2 = c2_ini + (c2_fin - c2_ini)*d/K; for i = 1:n % 依次更新第i个粒子的速度与位置 v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)); % 更新第i个粒子的速度 % 如果粒子的速度超过了最大速度限制,就对其进行调整 for j = 1: narvs if v(i,j) < -vmax(j) v(i,j) = -vmax(j); elseif v(i,j) > vmax(j) v(i,j) = vmax(j); end end x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun2(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun2(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun2(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun2(gbest); % 更新第d次迭代得到的最佳的适应度 pause(0.1) % 暂停0.1s h.XData = x(:,1); % 更新散点图句柄的x轴的数据(此时粒子的位置在图上发生了变化) h.YData = x(:,2); % 更新散点图句柄的y轴的数据(此时粒子的位置在图上发生了变化) h.ZData = fit; % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun2(gbest)) 9.改进:自动退出迭代循环
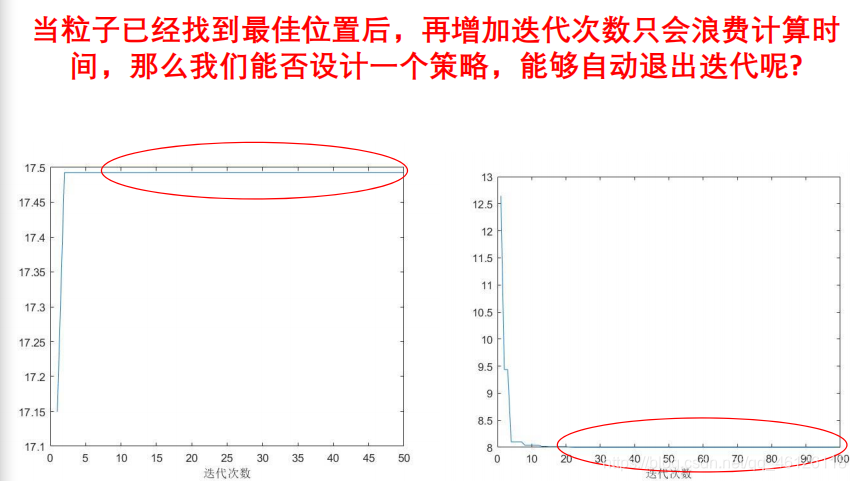
%% 自适应权重且带有收缩因子的粒子群算法PSO: 求解四种不同测试函数的最小值(动画演示)clear; clc%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)tic % 开始计时n = 1000; % 粒子数量narvs = 30; % 变量个数c1 = 2.05; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2.05; % 每个粒子的社会学习因子,也称为社会加速常数C = c1+c2; fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子w_max = 0.9; % 最大惯性权重,通常取0.9w_min = 0.4; % 最小惯性权重,通常取0.4K = 1000; % 迭代的次数% Sphere函数% vmax = 30*ones(1,30); % 粒子的最大速度% x_lb = -100*ones(1,30); % x的下界% x_ub = 100*ones(1,30); % x的上界% Rosenbrock函数vmax = 10*ones(1,30); % 粒子的最大速度x_lb = -30*ones(1,30); % x的下界x_ub = 30*ones(1,30); % x的上界% Rastrigin函数% vmax = 1.5*ones(1,30); % 粒子的最大速度% x_lb = -5.12*ones(1,30); % x的下界% x_ub = 5.12*ones(1,30); % x的上界% Griewank函数% vmax = 150*ones(1,30); % 粒子的最大速度% x_lb = -600*ones(1,30); % x的下界% x_ub = 600*ones(1,30); % x的上界%% 改进:自动退出迭代循环Count = 0; % 计数器初始化为0max_Count = 30; % 最大计数值初始化为30tolerance = 1e-6; % 函数变化量容忍度,取10^(-6)%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun3(x(i,:)); % 调用Obj_fun3函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 迭代K次来更新速度与位置% fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度% 注意我把上面这行注释掉了,因为我们不知道最后一共要迭代多少次,可能后面会自动跳出循环% 初始化的目的一般是节省运行的时间,在这里这个初始化的步骤我们可以跳过for d = 1:K % 开始迭代,一共迭代K次 tem = gbest; % 将上一步找到的最佳位置保存为临时变量 for i = 1:n % 依次更新第i个粒子的速度与位置 f_i = fit(i); % 取出第i个粒子的适应度 f_avg = sum(fit)/n; % 计算此时适应度的平均值 f_min = min(fit); % 计算此时适应度的最小值 if f_i <= f_avg w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min); else w = w_max; end v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:))); % 更新第i个粒子的速度 x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun3(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun3(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun3(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun3(gbest); % 更新第d次迭代得到的最佳的适应度 delta_fit = abs(Obj_fun3(gbest) - Obj_fun3(tem)); % 计算相邻两次迭代适应度的变化量 if delta_fit < tolerance % 判断这个变化量和“函数变化量容忍度”的相对大小,如果前者小,则计数器加1 Count = Count + 1; else Count = 0; % 否则计数器清0 end if Count > max_Count % 如果计数器的值达到了最大计数值 break; % 跳出循环 endendfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun3(gbest))toc % 结束计时 七.优化问题的测试函数

%% 自适应权重且带有收缩因子的粒子群算法PSO: 求解四种不同测试函数的最小值(动画演示)clear; clc%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)tic % 开始计时n = 1000; % 粒子数量narvs = 30; % 变量个数c1 = 2.05; % 每个粒子的个体学习因子,也称为个体加速常数c2 = 2.05; % 每个粒子的社会学习因子,也称为社会加速常数C = c1+c2; fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子w_max = 0.9; % 最大惯性权重,通常取0.9w_min = 0.4; % 最小惯性权重,通常取0.4K = 1000; % 迭代的次数% Sphere函数vmax = 30*ones(1,30); % 粒子的最大速度x_lb = -100*ones(1,30); % x的下界x_ub = 100*ones(1,30); % x的上界% Rosenbrock函数% vmax = 10*ones(1,30); % 粒子的最大速度% x_lb = -30*ones(1,30); % x的下界% x_ub = 30*ones(1,30); % x的上界% Rastrigin函数% vmax = 1.5*ones(1,30); % 粒子的最大速度% x_lb = -5.12*ones(1,30); % x的下界% x_ub = 5.12*ones(1,30); % x的上界% Griewank函数% vmax = 150*ones(1,30); % 粒子的最大速度% x_lb = -600*ones(1,30); % x的下界% x_ub = 600*ones(1,30); % x的上界%% 初始化粒子的位置和速度x = zeros(n,narvs);for i = 1: narvs x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内endv = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])%% 计算适应度fit = zeros(n,1); % 初始化这n个粒子的适应度全为0for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度 fit(i) = Obj_fun3(x(i,:)); % 调用Obj_fun3函数来计算适应度end pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)%% 迭代K次来更新速度与位置fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度for d = 1:K % 开始迭代,一共迭代K次 for i = 1:n % 依次更新第i个粒子的速度与位置 f_i = fit(i); % 取出第i个粒子的适应度 f_avg = sum(fit)/n; % 计算此时适应度的平均值 f_min = min(fit); % 计算此时适应度的最小值 if f_i <= f_avg w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min); else w = w_max; end v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:))); % 更新第i个粒子的速度 x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置 % 如果粒子的位置超出了定义域,就对其进行调整 for j = 1: narvs if x(i,j) < x_lb(j) x(i,j) = x_lb(j); elseif x(i,j) > x_ub(j) x(i,j) = x_ub(j); end end fit(i) = Obj_fun3(x(i,:)); % 重新计算第i个粒子的适应度 if fit(i) < Obj_fun3(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度 pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置 end if fit(i) < Obj_fun3(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度 gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置 end end fitnessbest(d) = Obj_fun3(gbest); % 更新第d次迭代得到的最佳的适应度endfigure(2) plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图xlabel('迭代次数');disp('最佳的位置是:'); disp(gbest)disp('此时最优值是:'); disp(Obj_fun3(gbest))toc % 结束计时 转载地址:http://xafg.baihongyu.com/
你可能感兴趣的文章
MTK Android 如何获取系统权限
查看>>
MySQL - 4种基本索引、聚簇索引和非聚索引、索引失效情况、SQL 优化
查看>>
MySQL - ERROR 1406
查看>>
mysql - 视图
查看>>
MySQL - 解读MySQL事务与锁机制
查看>>
mysql 1264_关于mysql 出现 1264 Out of range value for column 错误的解决办法
查看>>
mysql 1593_Linux高可用(HA)之MySQL主从复制中出现1593错误码的低级错误
查看>>
mysql ansi nulls_SET ANSI_NULLS ON SET QUOTED_IDENTIFIER ON 什么意思
查看>>
MySQL Binlog 日志监听与 Spring 集成实战
查看>>
Mysql Can't connect to MySQL server
查看>>
mysql case when 乱码_Mysql CASE WHEN 用法
查看>>
Multicast1
查看>>
MySQL Cluster 7.0.36 发布
查看>>
Multimodal Unsupervised Image-to-Image Translation多通道无监督图像翻译
查看>>
multipart/form-data与application/octet-stream的区别、application/x-www-form-urlencoded
查看>>
mysql cmake 报错,MySQL云服务器应用及cmake报错解决办法
查看>>
Multiple websites on single instance of IIS
查看>>
mysql CONCAT()函数拼接有NULL
查看>>
multiprocessing.Manager 嵌套共享对象不适用于队列
查看>>
multiprocessing.pool.map 和带有两个参数的函数
查看>>